循环结构（未完）

发表于 更新于 分类于 阅读次数： 阅读次数： 本文字数： 8.4k 阅读时长 ≈ 8 分钟

找最小值

给出 .n 和 .n 个整数ai ，求这 n 个整数中最小值是什么。

输入格式

第一行输入一个正整数 n，表示数字个数。

第二行输入 n 个非负整数，表示 a1 ,a2 …..an，以空格隔开。

输出格式

输出一个非负整数，表示这 n 个非负整数中的最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
int main(){
    int n,i,num;
    scanf("%d",&n);
    int a[n];
    for(i=0;i<n;i++)
    {
    	scanf("%d",&a[i]);
    	if(i==0) num=a[0];
    	if(a[i]<num) num=a[i];
	}
	printf("%d",num);
	return 0;
}

分类平均

给定 n 和 k，将从 1 到 n 之间的所有正整数可以分为两类：A 类数可以被 k 整除（也就是说是 k 的倍数），而 B 类数不能。请输出这两类数的平均数，精确到小数点后 1 位，用空格隔开。

数据保证两类数的个数都不会是 0。

输入格式

输入两个正整数 n 与 k。

输出格式

输出一行，两个实数，分别表示 A 类数与 B 类数的平均数。精确到小数点后一位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
int main(){
    int n,k,i,num=0;
    float a,b;
    scanf("%d %d",&n,&k);
    for(i=1;i<=n;i++)   //累加
    {
    	if(i%k==0) {a+=i;num=num+1;} 
		else{b+=i;}
	}
	if(k>n) {num=1;	n=n+1;} //如果k>n，完善代码
	a=a/(float)num;         //取平均数。
	b=b/(float)(n-num);
	printf("%.1f %.1f",a,b);
	return 0;
}

仍未通过洛谷测试点。

一尺之棰

《庄子》中说到，“一尺之棰，日取其半，万世不竭”。第一天有一根长度为 a 的木棍，从第二天开始，每天都要将这根木棍锯掉一半（每次除 2，向下取整）。第几天的时候木棍的长度会变为 1？

输入格式

输入一个正整数 a，表示木棍长度。

输出格式

输出一个正整数，表示要第几天的时候木棍长度会变为 1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
int main(){
    int a,k,i,num=0;
    scanf("%d",&a);
    if(a==1) num=1; //应付测试点，当a=1时，表示第1天木棍长度为1，若不加，则a=1时，第0天木棍长度为1。
    while(a-1)
    {
    	if(a%2&&a!=1) {a++;}
    	a=a/2;
    	num++;
	}
	printf("%d",num);
    return 0;
}

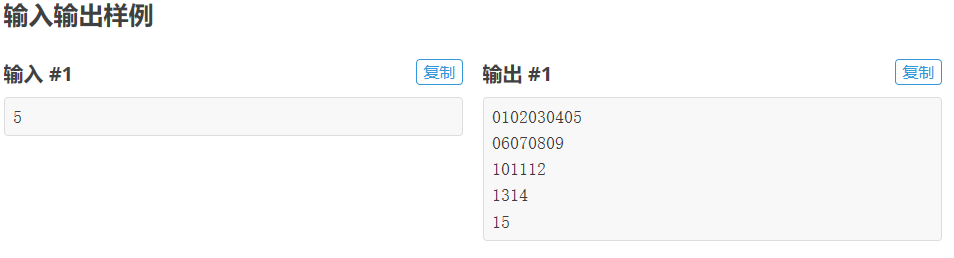
数字直角三角形

给出 n，请输出一个直角边长度是 n 的数字直角三角形。所有数字都是 2 位组成的，如果没有 2 位则加上前导 0。

输入格式

输入一个正整数 n。

输出格式

输出如题目要求的数字直角三角形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
int main(){
    int a,k,i,j,num=0;
    scanf("%d",&a);
    j=a;
    for(i=0;i<a;i++)
	{
			for(k=0;k<j;k++)
			{
				num++;
				printf("%02d",num);	
			}
			printf("\n");
			j--;	
	 } 
    return 0;
}

阶乘之和（高精度）

用高精度计算出!S=1!+2!+3!+⋯+n!（n*≤50）。

其中 ! 表示阶乘，定义为n*!=*n×(n−1)×(n−2)×⋯×1。例如，5!=5×4×3×2×1=120。

输入格式

一个正整数 n。

输出格式

一个正整数 S，表示计算结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
int main(){
    int a,i,j,k,x=1,num;
    scanf("%d",&a);
    k=a;
    for(i=0;i<a;i++)
    {
    	for(j=1;j<=k;j++)
	    {
	    	x=x*j;  //阶乘
		}
		num=x+num;  //求阶乘和
		k--;
		x=1;
	}
	printf("%d",num);
    return 0;
}

好吧好吧，还是想的太简单了。作为阶乘和，都是大整数，int和long甚至unsigned long long都无法存储。

那么拓展一下高精度的知识：

高精度乘法使用数组和逐位计算的方法来处理大整数乘法。每个数组元素存储整数的一位数字。通过使用数组来存储每个数字，可以处理任意长度的整数。

以下是高精度乘法的基本思路：

  1. 创建两个整数的数组表示乘法运算的两个操作数，每个数组元素存储一个数字位。
  2. 从低位开始，逐位相乘，并将结果累加到结果数组中的相应位置。
  3. 处理进位：如果某个位置的乘积结果大于等于10，则将进位部分加到高位上。
  4. 重复上述步骤，直到乘法运算完成。
  5. 最后，将结果数组转换为所需的输出格式。

高精度乘法的实现可能涉及到数组的遍历、进位处理和结果转换等操作。根据具体的需求和实现方式，代码可能会有所不同。在实际应用中，还可以使用现有的高精度计算库或使用其他更高效的算法来进行大整数乘法运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include <windows.h>
#include <stdio.h>
#include <math.h>

void AddStaff(void);
int StaffNum=0;
int Staff[10];
int main()
{
	AddStaff();
	return 0;
}


void AddStaff(void)  //添加员工 
{
	int i,j,a;
	printf("您需要录入几位员工的数据，请输入：");
	scanf("%d",&a);
	if(a<=0) {printf("ERROR！请输入正确的格式");}
	else
	{
		printf("开始录入员工编号\n");
		for(i=1;i<=a;i++)
		{
			printf("您正在录入第%d位员工的编号，输入完毕后请按回车键。\n",StaffNum+i);
			scanf("%d",&Staff[StaffNum+i]);
			for(j=1;j<StaffNum+i;j++)      //判断输入数据是否和之前的一样。 
			{
				if(Staff[StaffNum+i]==Staff[j])
				{
					printf("系统已收录该员工编号，请重新输入。\n"); 
					i--;	
				}	
			} 
		
			if(Staff[StaffNum+i]/10000000==0||Staff[StaffNum+i]/10000000>10)  //判断输入编号格式 
			{
				printf("请按照正确格式输入，该次输入无效。\n");
				i--;
			}
		} 
		printf("输入成功，已录入系统。");
		StaffNum+=a; 	
	}
} 

void LookStaff(void)   //查看录入的员工编号 
{
	int i;
	if(StaffNum==0)
	{
		printf("您还未录入员工编号，请先录入。");
	 } 
	 else
	 {
		 printf("以下是系统已录入的员工编号：");
		for(i=1;i<=StaffNum;i++)
		{
			printf("第%d位员工：",StaffNum);
			printf("%d\n",Staff[StaffNum]);
		}
	  } 

}

计数问题

题目描述

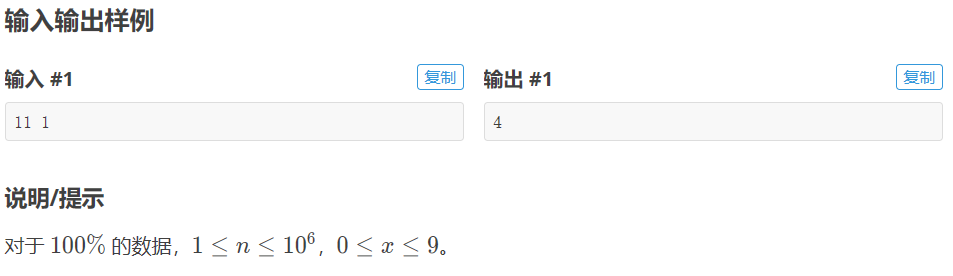
试计算在区间 1 到 n 的所有整数中，数字 x（0 ≤ x ≤ 9）共出现了多少次？例如，在 1 到 11 中，即在 1,2,3,4,5,6,7,8,9,10,11中，数字 1 出现了 4 次。

输入格式

2 个整数 n,x，之间用一个空格隔开。

输出格式

1 个整数，表示 x 出现的次数。

　　原本的想法是int两三个变量，用于存储n的每位数，比如123，存储为1,2,3，利用for循坏递增进位，每次个位数+1，都分别与x进行比对。but循环难写，而且n的输入范围达不到要求。

　　也想到一个较为巧妙的方法，比如x=1,当i（0 ≤ i ≤ 9）,x=i时，输出的y都为+1，当i>10,则x=i时，输出的y都为+2，因为10的十位都有1，所以个位+1时，y也要+1，以此类推。但是这种往后增加的方法，只能写固定的for循环，除非你真的写了很多很多很多很多个for循环，不然n的输入范围取决于你的for循坏和考虑的位数。

　　也想过用数组存储1234的每位数1,2,3,4。不过还是不太可行，直到我看题解，看到了一个很巧妙的方法。借此写出我的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<stdio.h>
int main()
{
	int n,x,y,i,a,b;
    scanf("%d %d",&n,&x);
    for(i=n;i>0;i--)
    {
    	b=i;
		while(b)
		{
			a=b%10;
			if(a==x) y++;
			b=b/10; 
		}    	
	}	
	printf("%d\n",y);
}

这个思路，很巧妙的将n“尾巴”进行“删减”，并提取出个位数进行比较。再通过for循环实行。

级数求和

题目描述

输入格式

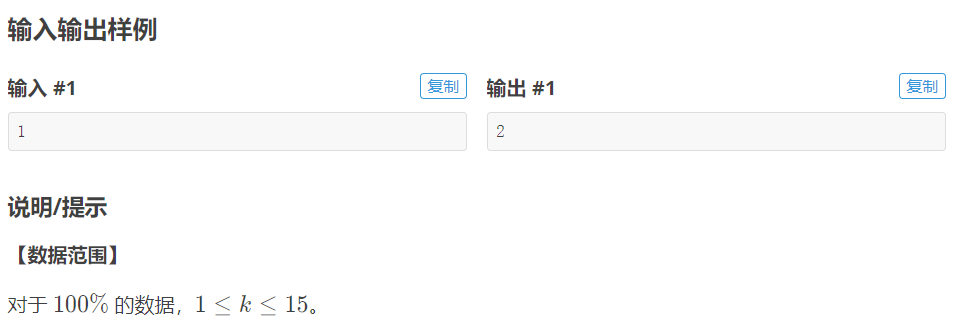
一个正整数k。

输出格式

一个正整数 n。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include<stdio.h>
int main()
{
	float s; 
	int i,k;
	scanf("%d",&k);
	while(1)
	{
		s=s+(1/(float)i);
		if((s-k)>0) break;
		i++;
	}
	printf("%d",i);
}

无法通过洛谷测试，经过chatgpt检查和提供的代码验证，代码的确可行，可能是超时了？但chatgpt的代码却通过了，还是在下面贴上它的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
int main() {
    int k;
    scanf("%d", &k);
    double Sn = 0.0;
    int n = 1;
    while (Sn <= k)
    {
        Sn += 1.0 / n;
        n++;
    }
    printf("%d\n",n - 1);
    return 0;
}

金币

题目描述

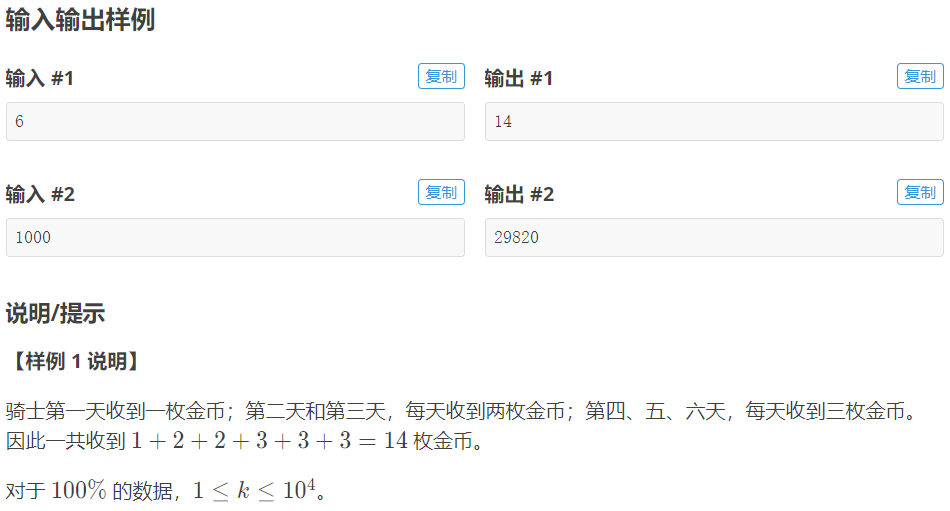
国王将金币作为工资，发放给忠诚的骑士。第一天，骑士收到一枚金币;之后两天(第二天和第三天)，每天收到两枚金币;之后三天(第四、五、六天)，每天收到三枚金币;之后四天(第七、八、九、十天)，每天收到四枚金币….这种工资发放模式会一直这样延续下去:当连续n天每天收到n枚金币后，骑士会在之后的连续n＋1天里，每天收到n＋1枚金币。

输入格式

—个正整数k，表示发放金币的天数。

输出格式

—个正整数，即骑士收到的金币数。

这简单，随便套几个循环暴力解决就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
int main()
{
	int k,i,n,num,x=1; 
	scanf("%d",&k);
	while(1)
	{
		for(i=x;i>0;i--)
		{
			n += x;
			num++;
			if(num==k) break;
		}
		x++;
		if(num==k) break;
	}
	printf("%d",n-1);
}

不过时间复杂度太高了，无法通过，解决问题容易，优化难。这种循环的主要问题，是不知道循环的天数，如果这个能解决，就不必用while。

贴一个别人的答案吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#include<stdio.h>
int main()
{
    int k,i,j,t=0,s=0;
    scanf("%d",&k);
    for(i=1;i<=k;i++)          //其实就是简单模拟，这里的i表示的是多少轮
    {
        if(t+i<=k)              //如果下一轮没有超过k天，直接加平方
        {
            t+=i;                //记天数
            s+=i*i;
        }
        else if(t+i>k)            //如果下一轮超过k天，加这一轮与k的差乘当前轮数
        {
            s+=i*(k-t);
            break;
        }
    }
    printf("%d",s);
    return 0;
}

我的方法是逐层相加，并在每一步进行天数比较。其它的求解则是干脆完整的执行一轮又一轮，比如5天，先求出“1+2+2+3+3+3”，再减一个3.而我是“1+2+2+3+3”，每一步都进行的比较。看来还是太暴力了，懒~

数列求和

题目描述

计算1＋2＋3＋·…＋(n - 1)＋n的值，其中正整数n不大于100。由于你没有高斯聪明，所以你不被允许使用等差数列求和公式直接求出答案。

输入格式

输入一个正整数n。

输出格式

输出一个正整数，表示最后求和的答案。

1
2
3
4
5
6
7
8
9
10
11
#include <stdio.h>
int main() {
    int i,n,num=0;
    scanf("%d", &n);
	for(i=n;i>0;i--)
	{
		num+=i;
	}
    printf("%d\n",num);
    return 0;
}

质数口袋

题目描述

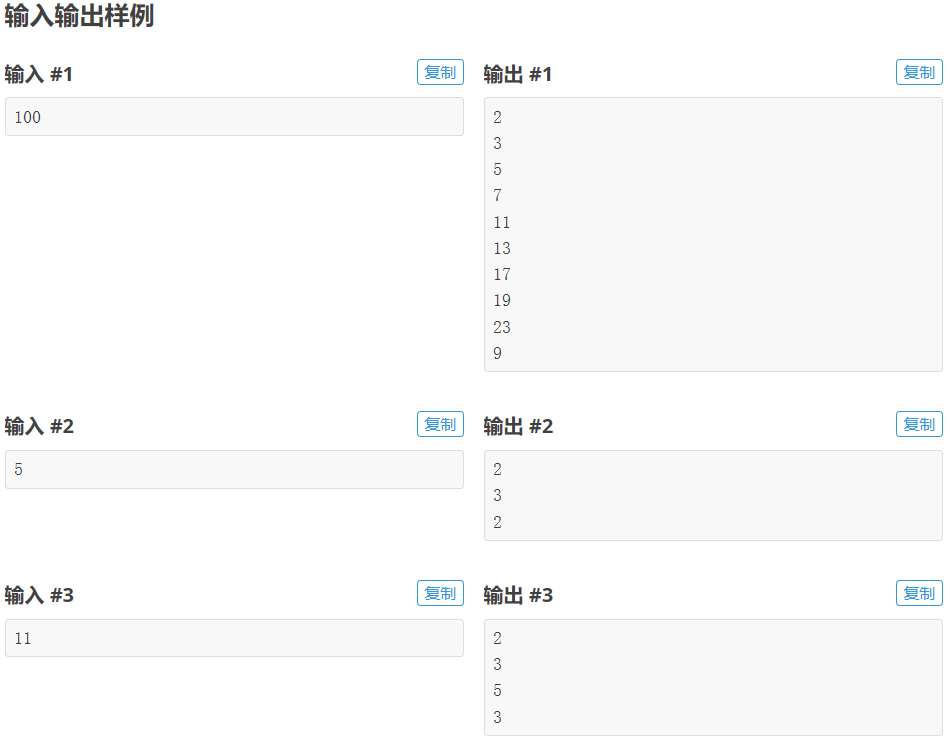
小A有一个质数口袋，里面可以装各个质数。他从2开始，依次判断各个自然数是不是质数，如果是质数就会把这个数字装入口袋。口袋的负载量就是口袋里的所有数字之和。但是口袋的承重量有限，装的质数的和不能超过L。给出L，请问口袋里能装下几个质数？将这些质数从小往大输出，然后输出最多能装下的质数的个数，数字之间用换行隔开。

输入格式

—行一个正整数L。

输出格式

将这些质数从小往大输出，然后输出最多能装下的质数个数，所有数字之间有一空行。

我只知道质数只能除1和它本身，并利用这点进行质数计算，存储到数组。当发现新的质数时，将对质数数组的和进行计算，并与输入进行比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdio.h>

int main() 
{
    int i,n,num,a[50],x=2,y,flag;
    scanf("%d",&n);
    while(1)
	{
		for(i=x-1;i>1;i--)
		{
			if((x%i)==0) flag=1; //判断是否为质数的标志位，不是质数标志位置1； 
		}
		if(flag==0)            //如果发现新的质数，将存放至数组并计算已有质数和。 
		{
			a[y]=x;
			for(i=y;i>=0;i--)
			{
				num = num+a[i];
			}
			y++;
		}
		flag = 0;
		if(num>n)  break;   //质数和与输入比较，达到要求就结束循环。 
		num = 0 ;
		x++;
	}  
    if(n==2)  y++;         //处理特例
	for(i=0;i<y-1;i++)    //按需输出
	{
		printf("%d\n",a[i]);
	}
	printf("%d",y-1);
}

好吧，尽管有效，但是无法通过洛谷的编译（真的，等我做完这几个题库，以后就去力扣了，想着由浅入深。）看了答案区，才发现有个埃拉托斯特尼筛法。好吧，这种方法的确高效，不必像我这样每个数进行判断。对于小范围的质数，达到题目的要求，我还是觉得我这个更好些。

而且题解区和贴吧没啥两样，不同的是贴吧真有大神。找不到简洁清晰的C语言埃氏筛，就先这样吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>

int main() 
{
    float a,b,s;
    int x;
    a=2;
    scanf("%f.1",&s);
    while(1)
    {
    	if(a>=s) break;
    	b=2*0.98;
    	a+=b;
    	x++;
	}
	printf("%d",x);
}