C语言函数

发表于 更新于 分类于 阅读次数： 阅读次数： 本文字数： 14k 阅读时长 ≈ 13 分钟
函数定义（C 语言自定义函数）

函数是一段可以重复使用的代码，用来独立地完成某个功能，它可以接收用户传递的数据，也可以不接收。接收用户数据的函数在定义时要指明参数，不接收用户数据的不需要指明，根据这一点可以将函数分为有参函数和无参函数。
将代码段封装成函数的过程叫做函数定义。

无参函数的定义

如果函数不接收用户传递的数据，那么定义时可以不带参数。如下所示：

1
2
dataType functionName(){
//body

dataType 是返回值类型，它可以是 C 语言中的任意数据类型，例如 int、 float、 char 等。
functionName 是函数名，它是标识符的一种，命名规则和标识符相同。函数名后面的括号( )不能少。
body 是函数体，它是函数需要执行的代码，是函数的主体部分。即使只有一个语句，函数体也要由{ }包围。
如果有返回值，在函数体中使用 return 语句返回。 return 出来的数据的类型要和 dataType 一样

无返回值函数
有的函数不需要返回值，或者返回值类型不确定（很少见），那么可以用 void 表示，例如： 

1
2
void hello() {
printf("Hello,world \n"); //没有返回值就不需要 return 语句 }

void 是 C 语言中的一个关键字，表示“空类型”或“无类型”，绝大部分情况下也就意味着没有 return 语句。

有参函数的定义

如果函数需要接收用户传递的数据，那么定义时就要带上参数。如下所示：

1
2
3
dataType functionName( dataType1 param1, dataType2 param2 ... ){
//body
}

dataType1 param1, dataType2 param2 …是参数列表。函数可以只有一个参数，也可以有多个，多个参数之间由,分隔。参数本质上也是变量，定义时要指明类型和名称。与无参函数的定义相比，有参函数的定义仅仅是多了一个参数列表。

数据通过参数传递到函数内部进行处理，处理完成以后再通过返回值告知函数外部。

例如：计算从 m 加到 n 的结果

1
2
3
4
5
6
7
int sum(int m, int n) {
    int i, sum = 0;
    for (i = m; i <= n; i++) {
        sum += i;
    }
    return sum;
}

调用 sum() 函数时，需要给它传递两份数据，一份传递给 m，一份传递给 n。你可以直接传递整数，例如：

1
int result = sum(1, 100); //1 传递给 m， 100 传递给 n

也可以传递变量：

1
2
3
int begin = 4;
int end = 86;
int result = sum(begin, end); //begin 传递给 m， end 传递给 n

也可以整数和变量一起传递：

1
2
int num = 33;
int result = sum(num, 80); //num 传递给 m， 80 传递给 n

函数定义时给出的参数称为形式参数，简称形参；函数调用时给出的参数（也就是传递的数据）称为实际参数，简称实参。函数调用时，将实参的值传递给形参，相当于一次赋值操作。
原则上讲，实参的类型和数目要与形参保持一致。如果能够进行自动类型转换，或者进行了强制类型转换，那么实参类型也可以不同于形参类型，例如将 int 类型的实参传递给 float 类型的形参就会发生自动类型转换。

函数不能嵌套定义

强调一点， C 语言不允许函数嵌套定义；也就是说，不能在一个函数中定义另外一个函数，必须在所有函数之外定义另外一个函数。 main() 也是一个函数定义，也不能在 main() 函数内部定义新函数。

函数不能嵌套定义，但可以嵌套调用，也就是在一个函数的定义或调用过程中允许出现对另外一个函数的调用。

函数的形参和实参
形参（形式参数）

在函数定义中出现的参数可以看做是一个占位符，它没有数据，只能等到函数被调用时接收传递进来的数据，所以称为形式参数，简称形参。

实参（实际参数）

函数被调用时给出的参数包含了实实在在的数据，会被函数内部的代码使用，所以称为实际参数，简称实参。
形参和实参的功能是传递数据，发生函数调用时，实参的值会传递给形参。

形参和实参的区别和联系

(1) 形参变量只有在函数被调用时才会分配内存，调用结束后，立刻释放内存，所以形参变量只有在函数内部有效，不能在函数外部使用。
(2) 实参可以是常量、变量、表达式、函数等，无论实参是何种类型的数据，在进行函数调用时，它们都必须有确定的值，以便把这些值传送给形参，所以应该提前用赋值、输入等办法使实参获得确定值。
(4) 实参和形参在数量上、类型上、顺序上必须严格一致，否则会发生“类型不匹配”的错误。当然，如果能够进行自动类型转换，或者进行了强制类型转换，那么实参类型也可以不同于形参类型。
(5) 函数调用中发生的数据传递是单向的，只能把实参的值传递给形参，而不能把形参的值反向地传递给实参；换句话说，一旦完成数据的传递，实参和形参就再也没有瓜葛了，所以，在函数调用过程中，形参的值发生改变并不会影响实参。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <stdio.h>
//计算从m加到n的值
int sum(int m, int n) {
    int i;
    for (i = m + 1; i <= n; ++i) {
        m += i;
    }
    return m;
}
int main() {
    int a, b, total;
    printf("Input two numbers: ");
    scanf("%d %d", &a, &b);
    total = sum(a, b);
    printf("a=%d, b=%d\n", a, b);
    printf("total=%d\n", total);
    return 0;
}

运行结果：
Input two numbers: 1 100↙
a=1, b=100
total=5050

在这段代码中，函数定义处的 m、 n 是形参，函数调用处的 a、 b 是实参。通过 scanf() 可以读取用户输入的数据，并赋值给 a、 b，在调用 sum() 函数时，这份数据会传递给形参 m、 n。

从运行情况看，输入 a 值为 1，即实参 a 的值为 1，把这个值传递给函数 sum() 后，形参 m 的初始值也为 1，在函数执行过程中，形参 m 的值变为 5050。函数运行结束后，输出实参 a 的值仍为 1，可见实参的值不会随形参的变化而变化。

以上调用 sum() 时是将变量作为函数实参，除此以外，你也可以将常量、表达式、函数返回值作为实参，如下所示：

1
2
3
total = sum(10, 98); //将常量作为实参
total = sum(a + 10, b - 3); //将表达式作为实参
total = sum(pow(2, 2), abs(-100)); //将函数返回值作为实参

(6) 形参和实参虽然可以同名，但它们之间是相互独立的，互不影响，因为实参在函数外部有效，而形参在函数内部有效。

函数声明以及函数原型

函数声明的格式非常简单，相当于去掉函数定义中的函数体，并在最后加上分号;，如下所示：

1
dataType functionName( dataType1 param1, dataType2 param2 ... );

也可以不写形参，只写数据类型：

1
dataType functionName( dataType1, dataType2 ... );

函数声明给出了函数名、返回值类型、参数列表（重点是参数类型）等与该函数有关的信息，称为函数原型（Function Prototype） 。函数原型的作用是告诉编译器与该函数有关的信息，让编译器知道函数的存在，以及存在的形式，即使函数暂时没有定义，编译器也知道如何使用它。

一般情况下，将函数定义放到 main() 的后面，将函数声明放到 main() 的前面，这样就使得代码结构清晰明了，主次分明。

C 语言变量的作用域

变量的作用域由变量的定义位置决定，在不同位置定义的变量，它的作用域是不一样的。

函数内部定义的变量（局部变量）

在函数内部定义的变量，它的作用域也仅限于函数内部，出了函数就不能使用了，我们将这样的变量称为局部变量（Local Variable） 。函数的形参也是局部变量，也只能在函数内部使用。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#include <stdio.h>
int sum(int m, int n){
    int i, sum=0;
    //m、 n、 i、 sum 都是局部变量，只能在 sum() 内部使用
    for(i=m; i<=n; i++){
        sum+=i;
    }
    return sum;
}
int main(){
    int begin = 5, end = 86;
    int result = sum(begin, end);
    //begin、 end、 result 也都是局部变量，只能在 main() 内部使用
    printf("The sum from %d to %d is %d\n", begin, end, result);
    return 0;
}

m、 n、 i、 sum 是局部变量，只能在 sum() 内部使用； begin、 end、 result 也是局部变量，只能在 main() 内部使用。
对局部变量的两点说明：
main() 也是一个函数，在 main() 内部定义的变量也是局部变量，只能在 main() 函数内部使用。

​ 形参也是局部变量，将实参传递给形参的过程，就是用实参给局部变量赋值的过程，它和 a=b; sum=m+n;这样的赋值没有什么区别

所有函数外部定义的变量（全局变量）

全局变量的默认作用域是整个程序，也就是所有的代码文件，包括源文件（.c 文件）和头文件（.h 文件） 。如果给全局变量加上 static 关键字，它的作用域就变成了当前文件，在其它文件中就无效了。

例：定义一个函数，根据长方体的长宽高求它的体积以及三个面的面积。 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
\#include <stdio.h>
//定义三个全局变量，分别表示三个面的面积
int s1 = 0, s2 = 0, s3 = 0;
int vs(int length, int width, int height){
    int v; //体积
    v = length * width * height;
    s1 = length * width;
    s2 = width * height;
    s3 = length * height;	
    return v;
}
int main(){
    int v = 0;
    v = vs(15, 20, 30);
    printf("v=%d, s1=%d, s2=%d, s3=%d\n", v, s1, s2, s3);
    v = vs(5, 17, 8);
    printf("v=%d, s1=%d, s2=%d, s3=%d\n", v, s1, s2, s3);
    return 0;
}

运行结果：
v=9000, s1=300, s2=600, s3=450
v=680, s1=85, s2=136, s3=40

通过变量的使用可以得到： 在一个函数内部修改全局变量的值会影响其它函数，全局变量的值在函数内部被修改后并不会自动恢复，它会一直保留该值，直到下次被修改。

C 语言规定，在同一个作用域中不能出现两个名字相同的变量，否则会产生命名冲突；但是在不同的作用域中，允许出现名字相同的变量，它们的作用范围不同，彼此之间不会产生冲突。这句话有两层含义：
不同函数内部可以出现同名的变量，不同函数是不同的局部作用域；
函数内部和外部可以出现同名的变量，函数内部是局部作用域，函数外部是全局作用域。

当函数内部的局部变量和函数外部的全局变量同名时，在当前函数这个局部作用域中，全局变量会被“屏蔽”，不再起作用。也就是说，在函数内部使用的是局部变量，而不是全局变量。

变量的使用遵循就近原则，如果在当前的局部作用域中找到了同名变量，就不会再去更大的全局作用域中查找。另外，只能从小的作用域向大的作用域中去寻找变量，而不能反过来，使用更小的作用域中的变量。

例如：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <stdio.h>
int n = 10; //全局变量
void func1(){
    int n = 20; //局部变量
    printf("func1 n: %d\n", n);
}
void func2(int n){
    printf("func2 n: %d\n", n);
}
void func3(){
    printf("func3 n: %d\n", n);
}
int main(){
    int n = 30; //局部变量
    func1();
    func2(n);
    func3();
    printf("main n: %d\n", n);
    return 0;
}

运行结果：

func1 n: 20
func2 n: 30
func3 n: 10
main n: 30

代码中虽然定义了多个同名变量 n，但它们的作用域不同，所有不会产生命名冲突。

下面是对输出结果的分析：
对于 func1()，输出结果为 20，显然使用的是 func1() 内部的 n，而不是外部的 n。
调用 func2() 时，会把 main() 中的实参 n 传递给 func2() 中的形参 n，此时形参 n 的值变为 30。形参 n 也
是局部变量，所以就使用它了。
func3() 输出 10，使用的是全局变量，因为在 func3() 中不存在局部变量 n，所以编译器只能到函数外部，也
就是全局作用域中去寻找变量 n。
main() 中 printf() 语句输出 30，说明使用的是 main() 中的 n，而不是外部的 n。

块级变量（在代码块内部定义的变量）

C 语言允许在代码块内部定义变量，这样的变量具有块级作用域；换句话说，在代码块内部定义的变量只能在代码块内部使用，出了代码块就无效了。

例如：

1
2
3
4
5
6
7
8
9
10
11
#include <stdio.h>
int main(){
    int n = 22; //编号①
    //由{ }包围的代码块
{
        int n = 40; //编号②
        printf("block n: %d\n", n);
}
    printf("main n: %d\n", n);
    return 0;
}

运行结果：
block n: 40
main n: 22

再谈作用域

示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <stdio.h>
int m = 13;
int n = 10;
void func1(){
    int n = 20;
{
        int n = 822;
        printf("block1 n: %d\n", n);
}
    printf("func1 n: %d\n", n);
}
void func2(int n){
    for(int i=0; i<10; i++){
        if(i % 5 == 0){
            printf("if m: %d\n", m);
        }else{
            int n = i % 4;
            if(n<2 && n>0){
                printf("else m: %d\n", m);
        }
    }
}
    printf("func2 n: %d\n", n);
}
void func3(){
    printf("func3 n: %d\n", n);
}
int main(){
    int n = 30;
    func1();
    func2(n);
    func3();  
    printf("main n: %d\n", n);
    return 0;
}

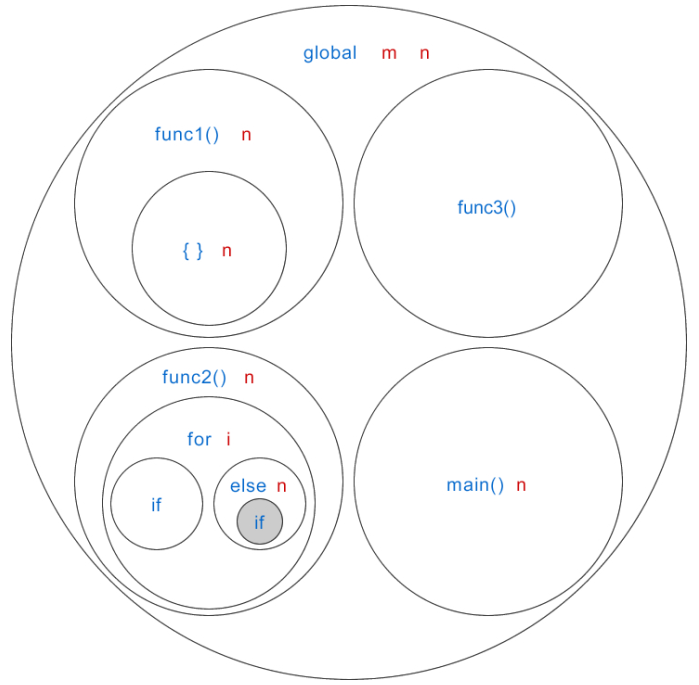
蓝色表示作用域的名称， 红色表示作用域中的变量， global 表示全局作用域。在灰色背景的作用域中，我们使用到了 m 变量，而该变量位于全局作用域中，所以得穿越好几层作用域才能找到 m。

递归函数（递归调用）

个函数在它的函数体内调用它自身称为递归调用，这种函数称为递归函数。执行递归函数将反复调用其自身，每调用一次就进入新的一层，当最内层的函数执行完毕后，再一层一层地由里到外退出。

以求阶乘为例，阶乘 n! 的计算公式如下：

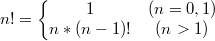
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
//求n的阶乘
long factorial(int n) {
    if (n == 0 || n == 1) {
        return 1;
}
    else {
        return factorial(n - 1) * n; // 递归调用
}
}
int main() {
    int a;
    printf("Input a number: ");
    scanf("%d", &a);
    printf("Factorial(%d) = %ld\n", a, factorial(a));
    return 0;
}

运行结果：
Input a number: 5↙
Factorial(5) = 120

factorial() 就是一个典型的递归函数。调用 factorial() 后即进入函数体，只有当 n==0 或 n==1 时函数才会执行结
束，否则就一直调用它自身。

由于每次调用的实参为 n-1，即把 n-1 的值赋给形参 n，所以每次递归实参的值都减 1，直到最后 n-1 的值为 1时再作递归调用，形参 n 的值也为 1，递归就终止了，会逐层退出。

下表列出了逐层进入的过程：

层次/层数 实参/形参 调用形式 需要计算的表达式 需要等待的结果
1 n=5 factorial(5) factorial(4) * 5 factorial(4) 的结果
2 n=4 factorial(4) factorial(3) * 4 factorial(3) 的结果
3 n=3 factorial(3) factorial(2) * 3 factorial(2) 的结果
4 n=2 factorial(2) factorial(1) * 2 factorial(1) 的结果
5 n=1 factorial(1) 1 无

当递归进入到最内层的时候，递归就结束了，就开始逐层退出了，也就是逐层执行 return 语句。

下表列出了逐层退出的过程

层次/层数 调用形式 需要计算的表达式 从内层递归得到的结果 （内层函数的返回值） 表达式的值 （当次调用的结果）
5 factorial(1) 1 无 1
4 factorial(2) factorial(1) * 2 factorial(1) 的返回值，也就是 1 2
3 factorial(3) factorial(2) * 3 factorial(2) 的返回值，也就是 2 6
2 factorial(4) factorial(3) * 4 factorial(3) 的返回值，也就是 6 24
1 factorial(5) factorial(4) * 5 factorial(4) 的返回值，也就是 24 120
递归的条件

每一个递归函数都应该只进行有限次的递归调用，否则它就会进入死胡同，永远也不能退出了，这样的程序是没有意义的。

要想让递归函数逐层进入再逐层退出，需要解决两个方面的问题：
存在限制条件，当符合这个条件时递归便不再继续。对于 factorial()，当形参 n 等于 0 或 1 时，递归就结束
了。
每次递归调用之后越来越接近这个限制条件。对于 factorial()，每次递归调用的实参为 n - 1，这会使得形参 n
的值逐渐减小，越来越趋近于 1 或 0。

中间递归函数

所谓中间递归，就是发生递归的位置在函数体的中间，而不是末尾。
尾递归在逐层退出时除了 return 语句，一般不再执行其他操作；而中间递归在逐层退出时还要执行一些其他的操作，所以比较复杂。

例如：字符串反转（逆置）函数 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <stdio.h>
#include <string.h>
//反转（逆置）字符串
char *reverse(char *str) {
    int len = strlen(str);
        if (len > 1) {
            char ctemp = str[0];
            str[0] = str[len - 1];
            str[len - 1] = '\0'; //最后一个字符在下次递归时不再处理
            reverse(str + 1); //递归调用
            str[len - 1] = ctemp;
    }
    return str;
}
int main() {
    char str[20] = "123456789";
    printf("%s\n", reverse(str));
    return 0;
}

运行结果：
987654321

每次调用函数，都会把字符串的第 0 个字符保存到 ctemp 变量，并把最后一个字符填充到第 0 个字符的位置，同时用’\0’来填充最后一个字符的位置。

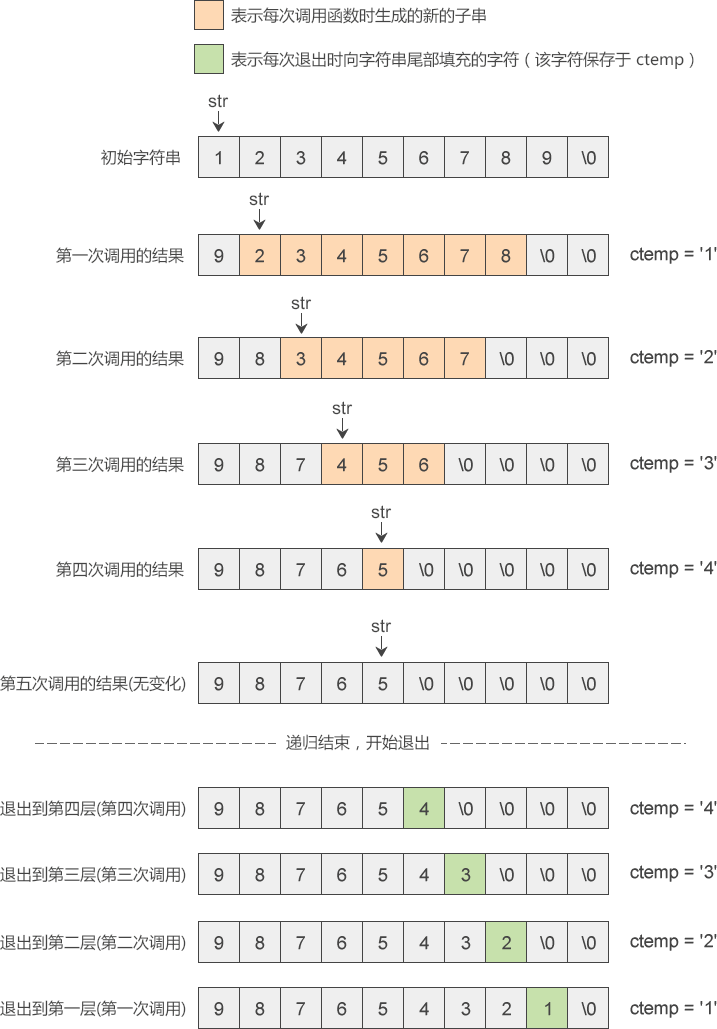
reverse() 的整体思路是，每次调用函数只交换字符串开头和末尾的两个字符，其它字符一律不管，并且这个交换过程也是分两个阶段完成的：

在逐层进入递归的阶段， reverse() 只是把字符串的最后一个字符移动到最前边，但是并没有把最前边一个字符移动到最后边，而是把最前边的字符保存到 ctemp 变量。

在逐层退出递归的阶段， reverse() 才把 ctemp 变量中保存的字符放到字符串的最前边。

两个阶段相互合作，才能最终完成两个字符的交换。

多层递归函数

多层递归的调用关系比较复杂，整体上看起来像一颗倒立的树：对于双层递归，树的每个节点有两个分叉；对
于三层递归，树的每个节点有三个分叉；以此类推……
下面以「求菲波那契数」为例:

菲波那契数就是一个数列，数列中每个数的值就是它前面两个数的和，这种关系常常用以下形式进行描述：

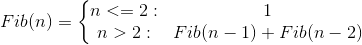
代码为：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <stdio.h>
//递归计算斐波那契数
long fib(int n) {
    if (n <= 2) {
        return 1;
    }
    else {
        return fib(n - 1) + fib(n - 2);
    }
}
int main() {
    int a;
    printf("Input a number: ");
    scanf("%d", &a);
    printf("Fib(%d) = %ld\n", a, fib(a));
    return 0;
}

运行结果：
Input a number: 7↙
Fib(7) = 13

当 n≥2 时，每次调用 fib(n) 都要等待 fib(n-1) 和 fib(n-2) 的结果，这种调用关系看起来就像一棵倒立的二叉树，如下图所示：

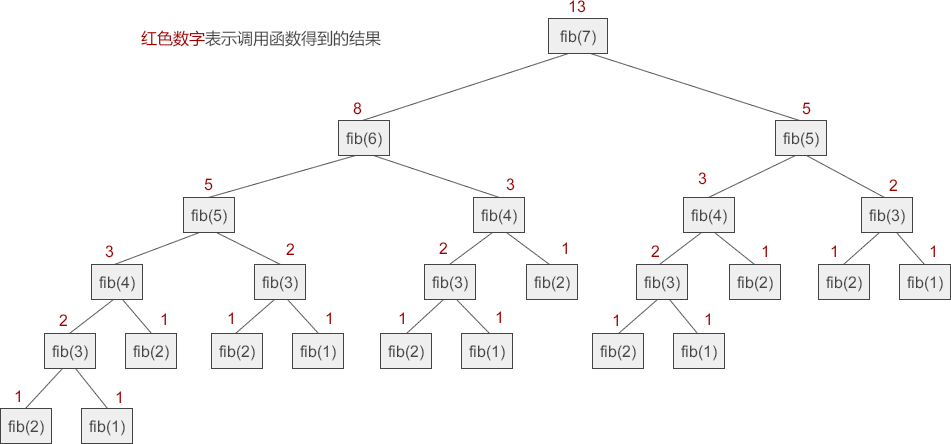
双层递归的调用关系和数据结构中二叉树的结构完全吻合，所以双层递归常用于二叉树的遍历。

单层递归每次只等待一个函数的结果，双层递归每次要等待两个函数的结果，这就是它们之间最本质的区别。

递归函数的缺陷和优化
递归函数的空间开销

递归函数内部嵌套了对自身的调用，除非等到最内层的函数调用结束，否则外层的所有函数都不会调用结束。

通俗地讲，外层函数被卡主了，它要等待所有的内层函数调用完成后，它自己才能调用完成。

每一层的递归调用都会在栈上分配一块内存， 有多少层递归调用就分配多少块相似的内存，所有内存加起来的总和是相当恐怖的，很容易超过栈内存的大小限制，这个时候就会导致程序崩溃。

例如，一个递归函数需要递归 10000 次，每次需要 1KB 的内存，那么最终就需要 10MB 的内存

递归函数的时间开销

每次调用函数都会在栈上分配内存，函数调用结束后再释放这一部分内存，内存的分配和释放都是需要时间的。
每次调用函数还会多次修改寄存器的值，函数调用结束后还需要找到上层函数的位置再继续执行，这也是需要时间的。

以「求斐波那契数」为例 ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <stdio.h>
#include <time.h>   
// 递归计算斐波那契数
long fib(int n) {
    if (n <= 2) {
        return 1;
    }
    else {
        return fib(n - 1) + fib(n - 2);
    }
}
int main() {
int a;
    clock_t time_start, time_end;
    printf("Input a number: ");
    scanf("%d", &a);
    time_start = clock();
    printf("Fib(%d) = %ld\n", a, fib(a));
    time_end = clock();
    printf("run time: %lfs\n", (double)(time_end - time_start)/ CLOCKS_PER_SEC );
    return 0;
}

运行结果：
Input a number: 42↙
Fib(42) = 267914296
run time: 0.833000s

可以看到，求 42 的斐波那契数程序所用的时间为 0.83 秒。

使用迭代来替换递归函数

递归函数应为原理层面的缺陷，无法优化，但大部分能用递归解决的问题也能用迭代来解决。所谓迭代，就是循环。

许多问题是以递归的形式进行解释的，这只是因为它比非递归形式更为清晰。但是， 这些问题的迭代实现往往比递归实现效率更高，虽然代码的可读性可能稍差一些。

还是以求斐波那契数为例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <stdio.h>
#include <time.h>
//递归计算斐波那契数
long fib_recursion(int n) {
    if (n <= 2) {
        return 1;
    }
    else {
        return fib_recursion(n - 1) + fib_recursion(n - 2);
    }
}
//迭代计算斐波那契数
long fib_iteration(int n){
    long result;
    long previous_result;
    long next_older_result;
    result = previous_result = 1;
    while (n > 2) {
        n -= 1;
        next_older_result = previous_result;
        previous_result = result;
        result = previous_result + next_older_result;
    }
        return result;
}
int main() {
    int a;
    clock_t time_start_recursion, time_end_recursion;
    clock_t time_start_iteration, time_end_iteration;
    printf("Input a number: ");
    scanf("%d", &a);
    //递归的时间
    time_start_recursion = clock();
    printf("Fib_recursion(%d) = %ld\n", a, fib_recursion(a));
    time_end_recursion = clock();
    printf("run time with recursion: %lfs\n", (double)(time_end_recursion -
    time_start_recursion)/ CLOCKS_PER_SEC );
    //迭代的时间
    time_start_iteration = clock();
    printf("Fib_iteration(%d) = %ld\n", a, fib_iteration(a));
    time_end_iteration = clock();
    printf("run time with iteration: %lfs\n", (double)(time_end_iteration - time_start_iteration)
    / CLOCKS_PER_SEC);
    return 0;
}

运行结果

Input a number: 42
Fib_recursion(42) = 267914296
run time with recursion: 0.854000s
Fib_iteration(42) = 267914296
run time with iteration: 0.000000s

可以看出迭代还是比递归快一点点的。